Sir Isaac Newton, durante su retiro en una granja de Woolsthorpe durante los años 1665-1666 elaboró la base de lo que hoy se conoce como la ley de gravitación universal, basándose en las leyes de Kepler sobre el movimiento de los planetas y los estudios de Galileo.

Esta ley establece que los cuerpos, por el simple hecho de tener masa, experimentan una fuerza de atracción hacia otros cuerpos con masa, denominada fuerza gravitatoria o fuerza gravitacional. Esta fuerza, explica entre otras muchas cosas, por qué orbitan los planetas.

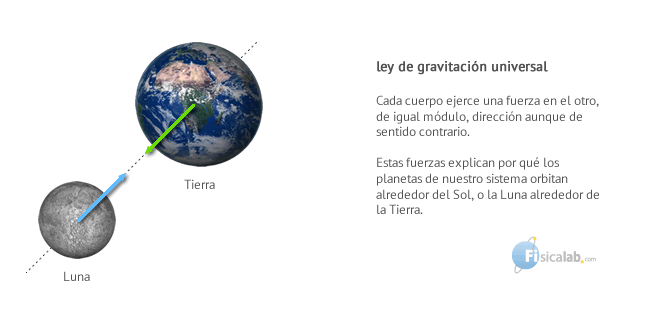
La fuerza gravitacional entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Matemáticamente se expresa de la siguiente forma:

F→g=−G⋅M⋅mr2⋅u→r

donde:

• G es la constante de gravitación universal, G = 6,67·10-11 N·m2/kg2
• M y m son las masas de los cuepos que interaccionan
• r es la distancia que los separa.
• u→r es un vector unitario que expresa la dirección de actuación de la fuerza.

De igual forma, el módulo de dicha fuerza se puede obtener mediante la siguiente ecuación:

Fg=G⋅M⋅mr2

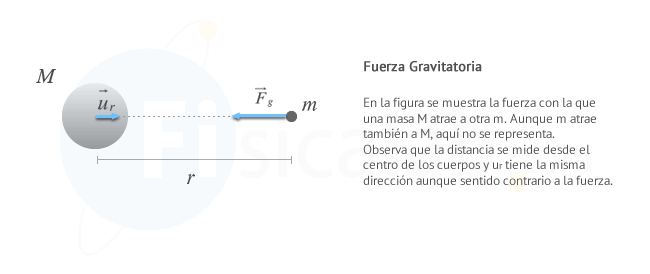
Ambas expresiones de la ley de la gravitación universal, únicamente sirven para masas puntuales y cuerpos esféricos, ya que estos se comportan como si toda su masa se concentrara en su centro. Por tanto, la distancia se mide desde sus centros.

Realizado por: Gonzalo Terrón Luque